
Language models small enough to run on edge devices like a laptop, tablet or phone can now employ a technique given away by Microsoft Asia this week called rStar-Math. Small language models with as few as 3 Billion parameters were able to compete with oh-so-recently state-of-the-art models like o1-preview on various mathematics benchmarks. That is to say, at the standard of a world class math prodigy.
Imagine the 2% of the the total 17 million US high school students, or the best 300,000 who are selected to compete in the American Mathematics Competitions. This is already the top math talent we can muster at this age; I don’t think I personally knew anyone in school talented enough to compete in the AMC, much less the USA Math Olympiad. Microsoft’s method allowed a 7 billion parameter model to achieve a score beat 99.53% of those nerds, as it was able to solve 8 out of 15 of the problems on the USA Math Olympiad 2024, a score comparable to the top 20% of competing Olympians.
Basically, I’ll probably never meet anyone who can perform high level mathematics better than these open source models after just 4 rounds of self-play. These models are quite affordable to run, and freely accessible.
Here’s what it cost them:

Based on this, the experiment likely consumed on the order of 50,000 GPU-hours, incurring a notional cost in the $100k–$200k range under typical cloud pricing. That’s simply remarkable!
Here’s the article: https://arxiv.org/abs/2501.04519
The code and data will be shared here: https://github.com/microsoft/rStar

rStar-Math enables a small language model to achieve better reasoning through a process called self-evolution.
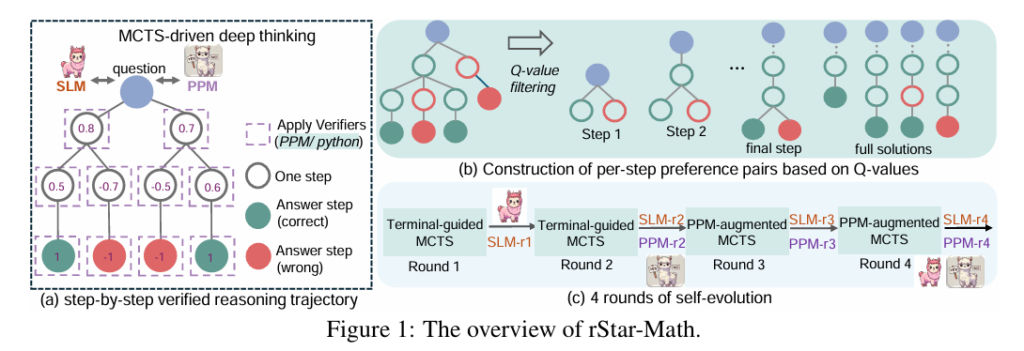
🧩 Step 1: Generating Solutions Using Monte Carlo Tree Search (MCTS)
- Instead of solving math problems in one go, the model uses Monte Carlo Tree Search (MCTS) to explore different solution paths step by step.
- At each step, it generates multiple possible next steps (nodes) and evaluates them.
🧩 Step 2: Evaluating Steps Using a Reward Model
- The system uses a Process Preference Model (PPM) to evaluate the quality of each step.
- The model assigns Q-values (scores) to each step based on whether it leads to a correct final answer.
🧩 Step 3: Learning Through Iterative Self-Evolution
The updated model becomes smarter with each round, learning to avoid common mistakes and focus on high-quality reasoning steps.
The model goes through multiple rounds of self-training.
Each round produces better-quality data (verified solution steps) that are used to retrain the model.
Selected highlights from the research paper:
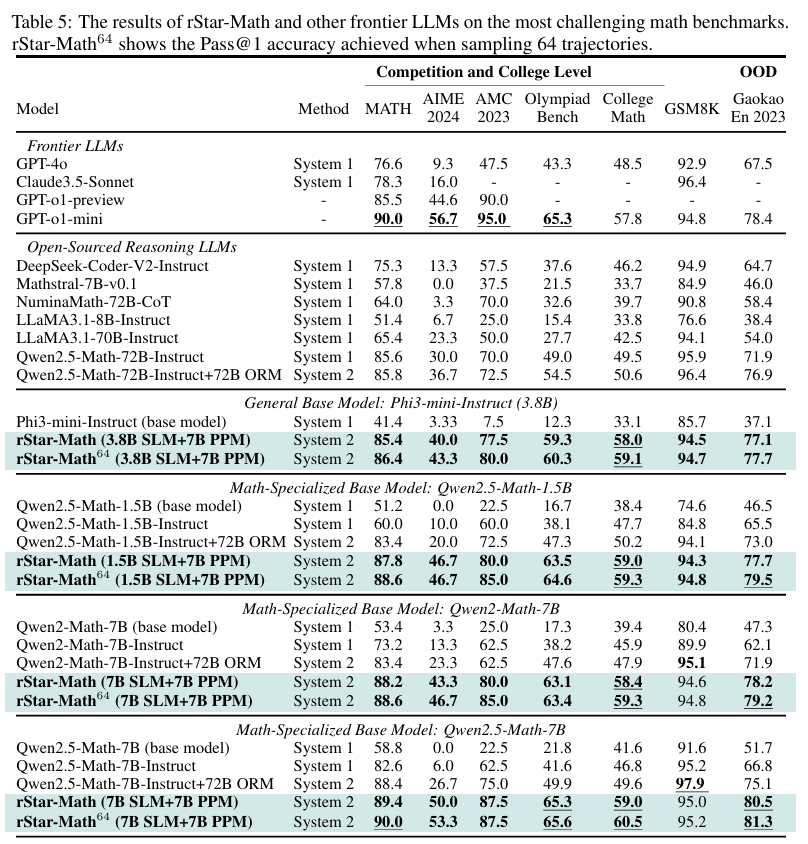
Benchmark results:
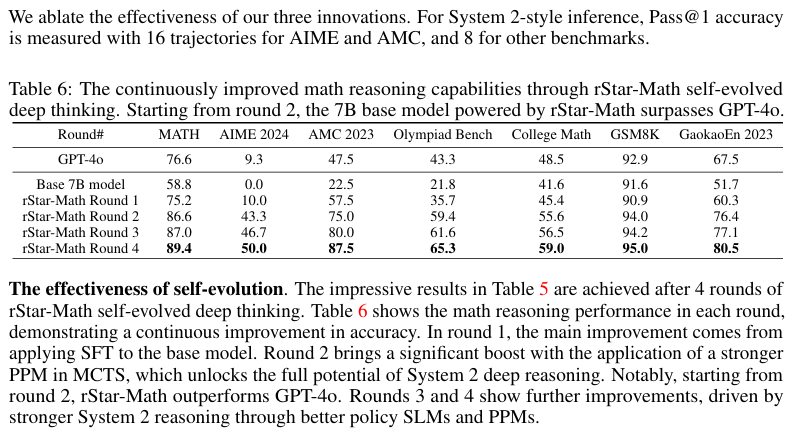
Benchmarks as measured after each round of evolution:
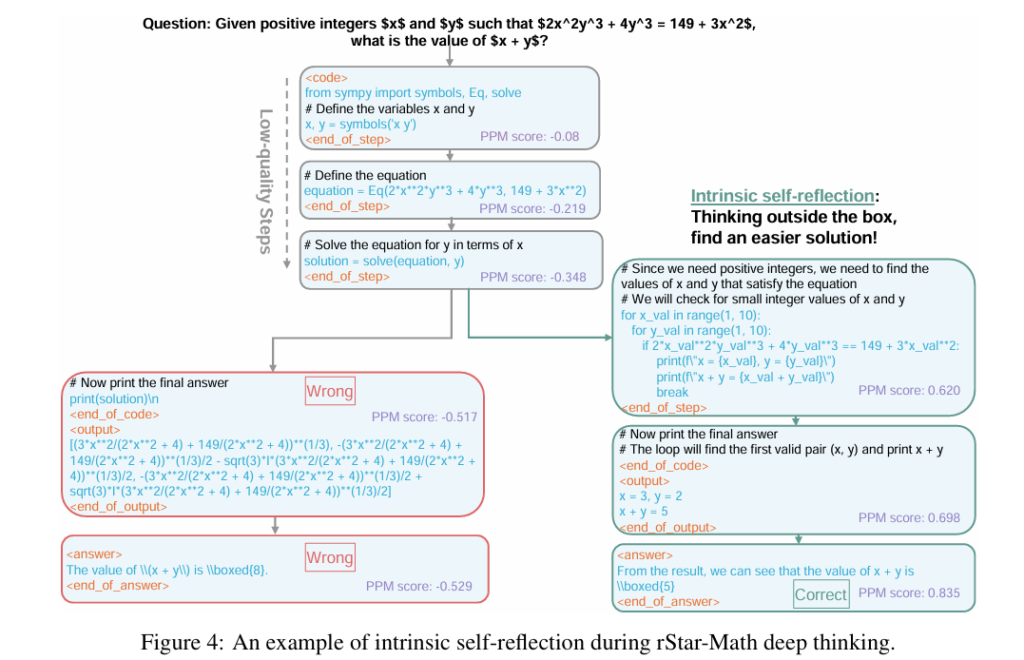
Interesting insight into the approach it takes:

Bigger picture:

The example problem proof mentioned above re: generalization:

One more example:
